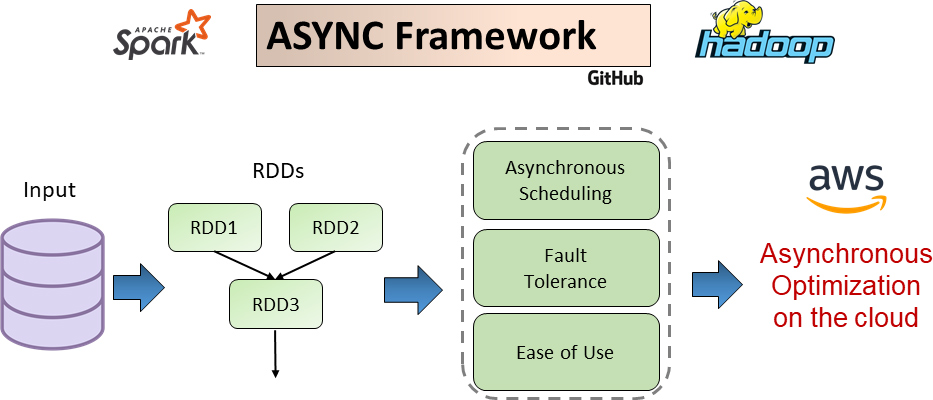
ScaleML
Machine Learning at Scale!
We improve the scalability and performance of machine learning applications on parallel and cloud computing platforms. Our approach targets both theoretical aspects and systems engineering. Optimization algorithms are reformulated to reduce communication and computation costs in large scale data processing. We also develop novel systems that support stochastic and asynchronous execution of big data applications on cloud computing platforms.
NASOQ
Large-scale linear and non-linear optimization methods are frequently used in applications such as computer graphics and machine learning. Existing implementations of these algorithms are either not scalable or not accurate or not fast. We develop novel algorithms and systems that significantly improve the performance of optimization methods in applications such as computer graphics and geometry processing. For example, our NASOQ solver improves the performance of computer graphics simulations with quadratic programs (QP) up to 24 times compared to the fastest competing solvers and is more accurate than the competitors.
- PUBLICATIONS:
NASOQ
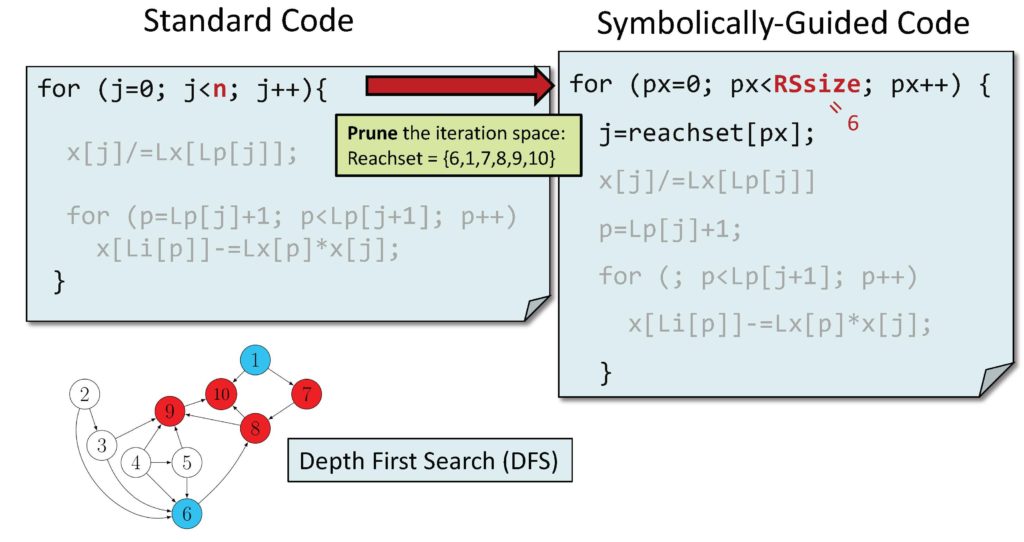
Compiler Design and Verification
Sparse matrix computations are at the heart of many scientific and data mining codes. We build sparse matrix code generators by developing domain-specific compilers, novel verification techniques for compiler transformations, and programming languages. We demonstrate the practical application of sparse matrix code generation for applications such as computer graphics, machine learning, and robotics.
MatRox
Approximate Matrix Algorithms for Machine Learning
A large class of applications in machine learning and scientific computing, such as statistical learning kernel methods and integral equations often operate on dense matrices with structure. The storage costs and computation complexity of operating on large dense matrices makes the use of deterministic matrix computations infeasible in many scenarios. However, when the problem has structure, randomized algorithms and low-rank approximation methods give tractable approximations with rigorous guarantees for many matrix computations. We build high-performance frameworks that automatically analyze the input structure to efficiently compress and approximate the matrix computations while satisfying user-specific accuracies.
TesCo
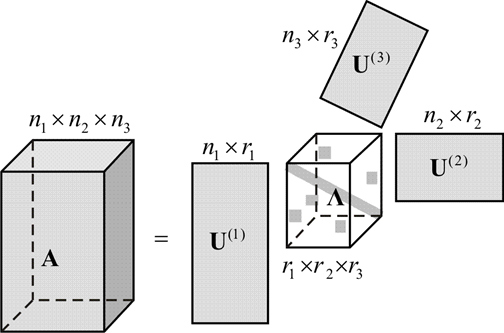
Scalable Tensor Computations
Tensor decomposition algorithms appear in numerous domains and applications such as data mining, machine learning and computer vision. Sparse tensor algorithms are of particular interest in analyzing and compressing big datasets as most real-world data is sparse and multidimensional. However, state-of-the-art tensor algorithms are not scalable for overwhelmingly large and higher-order sparse tensors on parallel and distributed platforms. We implement novel algorithms that enable better scalability of tensor algorithms operating on large amounts of data on GPUs, cloud and distributed computing platforms.
NumCy
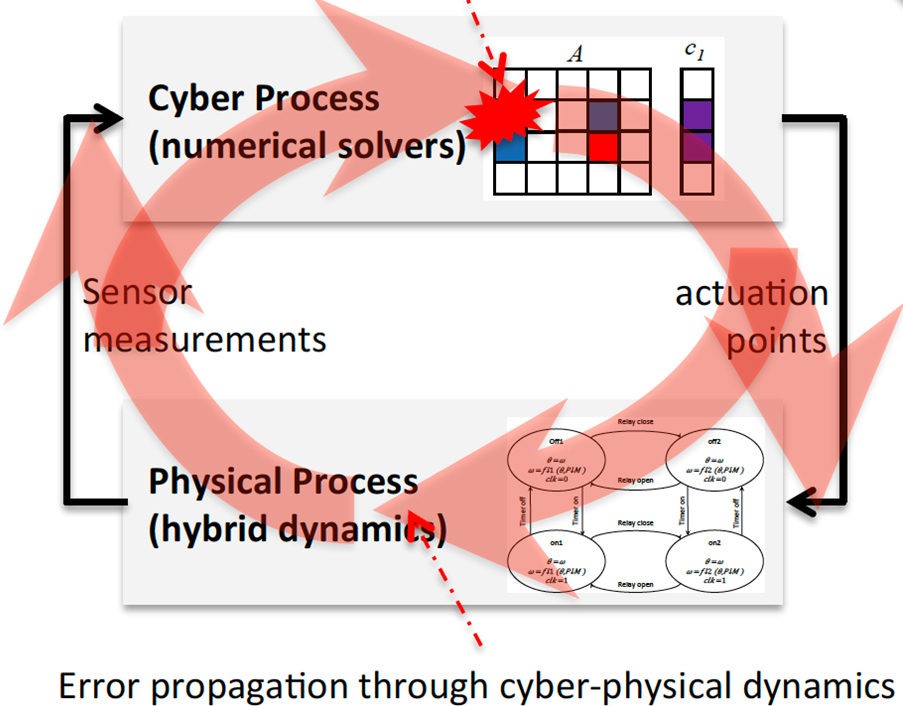
Cyber-Physical Security
Cyber physical systems (CPS) and internet of things (IoT) devices, such as automobiles, medical devices and drone controls, are the governing components and the core to critical infrastructure in the government and everyday life. Cyber attacks can cause various types of data integrity violations and disrupt the function of CPS and IOT devices. Malicious data corruption and errors injection may make the numerical methods and algorithms in the software produce incorrect results or increase runtime. The objective of this work is to investigate fundamental and mathematically rigorous solutions for security-oriented algorithmic hardening of commonly-used numerical methods and their implementations for cyber-physical critical infrastructures.